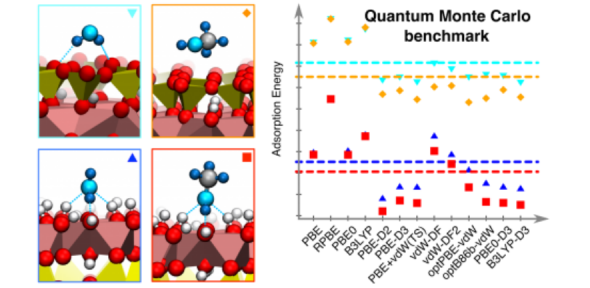
Density functional theory (DFT) is the workhorse of computational materials science. In principle it is exact but in practice it relies on an approximation for how electrons interact with each other. We are tackling the issue of the accuracy of DFT through extensive series of studies of small gas phase complexes [1], molecular crystals [2], [3], and molecules at solid interfaces [4]–[7] using methods beyond DFT, such as Quantum Monte Carlo (QMC) or Coupled Cluster with singles, doubles and perturbative triples [CCSD(T)].
The application of high-level methods such as QMC or CCSD(T) to the complex systems that are of interest to us comes with extreme computational burdens and in many cases, requires algorithmic or protocol developments. For QMC, the group has contributed towards algorithmic improvements to speed up the method by many orders of magnitude [8], [9] as well as developed a protocol for fast and accurate application on molecular crystals [3], [10]. For CCSD(T), the group has produced an efficient and accurate protocol for its application on defects and adsorbates on metal-oxide surfaces [11].
A major challenge for DFT is the accurate description of van der Waals interactions, and London dispersion, which is ubiquitous in nature, contributing to the binding of biomolecules such as DNA, molecular crystals, and adsorption of molecules on surfaces. Previously, we have worked to develop the class of optB88-vdW, optPBE-vdW, and optB86b-vdW functionals [12]–[14] to allow dispersion to be accounted for within DFT.
References:
[1] Y. S. Al-Hamdani et al., ‘Interactions between large molecules pose a puzzle for reference quantum mechanical methods’, Nat Commun, vol. 12, no. 1, p. 3927, Jun. 2021, doi: 10.1038/s41467-021-24119-3.
[2] J. Chen, A. Zen, J. G. Brandenburg, D. Alfè, and A. Michaelides, ‘Evidence for stable square ice from quantum Monte Carlo’, Phys. Rev. B, vol. 94, no. 22, p. 220102, Dec. 2016, doi: 10.1103/PhysRevB.94.220102.
[3] A. Zen, J. G. Brandenburg, J. Klimeš, A. Tkatchenko, D. Alfè, and A. Michaelides, ‘Fast and accurate quantum Monte Carlo for molecular crystals’, PNAS, vol. 115, no. 8, pp. 1724–1729, Feb. 2018, doi: 10.1073/pnas.1715434115.
[4] A. Zen et al., ‘Toward Accurate Adsorption Energetics on Clay Surfaces’, J. Phys. Chem. C, vol. 120, no. 46, pp. 26402–26413, Nov. 2016, doi: 10.1021/acs.jpcc.6b09559.
[5] J. G. Brandenburg et al., ‘Physisorption of Water on Graphene: Subchemical Accuracy from Many-Body Electronic Structure Methods’, J. Phys. Chem. Lett., vol. 10, no. 3, pp. 358–368, Feb. 2019, doi: 10.1021/acs.jpclett.8b03679.
[6] Y. S. Al-Hamdani, M. Ma, D. Alfè, O. A. von Lilienfeld, and A. Michaelides, ‘Communication: Water on hexagonal boron nitride from diffusion Monte Carlo’, J. Chem. Phys., vol. 142, no. 18, p. 181101, May 2015, doi: 10.1063/1.4921106.
[7] Y. S. Al-Hamdani, D. Alfè, and A. Michaelides, ‘How strongly do hydrogen and water molecules stick to carbon nanomaterials?’, J. Chem. Phys., vol. 146, no. 9, p. 094701, Mar. 2017, doi: 10.1063/1.4977180.
[8] A. Zen, J. G. Brandenburg, A. Michaelides, and D. Alfè, ‘A new scheme for fixed node diffusion quantum Monte Carlo with pseudopotentials: Improving reproducibility and reducing the trial-wave-function bias’, J. Chem. Phys., vol. 151, no. 13, p. 134105, Oct. 2019, doi: 10.1063/1.5119729.
[9] A. Zen, S. Sorella, M. J. Gillan, A. Michaelides, and D. Alfè, ‘Boosting the accuracy and speed of quantum Monte Carlo: Size consistency and time step’, Phys. Rev. B, vol. 93, no. 24, p. 241118, Jun. 2016, doi: 10.1103/PhysRevB.93.241118.
[10] F. Della Pia, A. Zen, D. Alfè, and A. Michaelides, ‘DMC-ICE13: ambient and high pressure polymorphs of ice from Diffusion Monte Carlo and Density Functional Theory’. arXiv, Jul. 04, 2022. doi: 10.48550/arXiv.2207.01353.
[11] B. X. Shi, V. Kapil, A. Zen, J. Chen, A. Alavi, and A. Michaelides, ‘General embedded cluster protocol for accurate modeling of oxygen vacancies in metal-oxides’, J. Chem. Phys., vol. 156, no. 12, p. 124704, Mar. 2022, doi: 10.1063/5.0087031.
[12] J. Klimeš, D. R. Bowler, and A. Michaelides, ‘Chemical accuracy for the van der Waals density functional’, J. Phys.: Condens. Matter, vol. 22, no. 2, p. 022201, Jan. 2010, doi: 10.1088/0953-8984/22/2/022201.
[13] J. Klimeš, D. R. Bowler, and A. Michaelides, ‘Van der Waals density functionals applied to solids’, Phys. Rev. B, vol. 83, no. 19, p. 195131, May 2011, doi: 10.1103/PhysRevB.83.195131.
[14] J. Klimeš and A. Michaelides, ‘Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory’, J. Chem. Phys., vol. 137, no. 12, p. 120901, Sep. 2012, doi: 10.1063/1.4754130.
